|
||||||||||||
|
КВАНТОВО-СТРУКТУРНЫЕ МОДЕЛИ & МАШИНЫ "Подвергай все сомнению." В работе описывается информационная модель физического мира на основе введенных автором понятий кванта структуры, квантово-структурного пространства, а также ряда функций и операций над ними. |
|
Введение. Традиционно считается, что основополагающими при описании закономерностей физического мира являются пространственно-временные и причинно-следственные отношения между явлениями природы и, следовательно, моделирование именно указанных отношений должно лежать в основе, как работы человеческого мозга, так и биологических нейронных сетей (БНС) в целом. Однако результаты многочисленных нейрофизиологических исследований не дают оснований сделать подобный вывод. В данной работе предлагается математическая модель описания отношений между явлениями физического мира альтернативная традиционному подходу в том смысле, что в основе моделирования лежат иные отношения. Любое явление природы можно рассматривать как триединую сущность (три различных и равноправных стороны одного и того же), а именно: 1) как нечто целое, что отличает его от других и, следовательно, имеет право на собственное уникальное имя; 2) как сложное, состоящее из частей других явлений; 3) как простое, являющееся частью сложного явления. Если в процессе анализа учитывать только одно выше указанное обстоятельство, то явления природы можно рассматривать как абстрактные однотипные объекты. Объединенные в иерархические структуры, они образуют некоторое пространство. Такое пространство, как известно, называют структурой. А поскольку это пространство состоит из дискретных элементов (частиц или квантов), то и называть его мы будем квантово-структурным пространством, а элементы пространства — квантами структуры. Отметим, что при указанном подходе такие различные физические явления как объект, признак, процесс и прочее, могут рассматриваться как представители единой "категории". Поэтому все явления физического мира мы будем обозначать термином Событие и наоборот, употребляя термины объект, признак, процесс, образ и т.д., будем иметь в виду, что все это в нашем понимании События. |
|
1. Квантово-структурная теория. (КСТ) 1.1. Понятие кванта структуры и квантово-структурного пространства. Пусть задано дискретное конечное пространство S взаимосвязанных между собой объектов (элементов) si О S , где: 1) для каждого элемента si определены два линейно-упорядоченных подмножества (цепочки) Ii и Oi произвольной длины, составленных из элементов того же пространства S; 2) задано отношение порядка такое, что sj < si < sk , если sj О Ii и sk О Oi ; 3) задано отношение равенства такое, что si = sj , если Ii = Ij ; 4) для любой пары элементов si , sj выполняется условие si № sj . Пространство S, удовлетворяющее условиям 1 — 4, будем называть квантово-структурным пространством (QSS), а элементы si — квантами (частицами) структуры (QS).
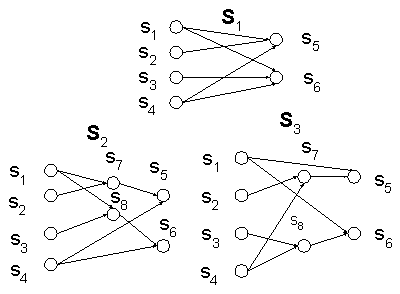
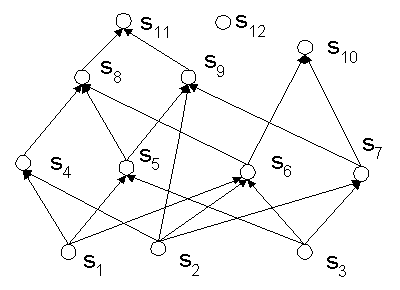
В ряде случаев QSS графически может быть изображено в виде графа, вершинами которого являются элементы si , а направление и порядок следования дуг соответствуют отношению порядка. Дуга направлена от вершины si к вершине sj , если si < sj и Oi З Ij № Ж. Условно примем, что порядок следования дуг, примыкающих к вершине графа, соответствует порядку следования элементов в цепочках: для Ii — против часовой стрелки; для Oi — по часовой стрелке. Из рис.1 видно, что с каждый элементом si можно сопоставить два подмножества из S, а именно подмножество Ii элементов sj определяющее входящие в вершину si связи и подмножество Oi элементов sk определяющее исходящие из вершины si связи. Определим QS как тройку: ( si / Ii / Oi ), (1.1) где Ii и Oi – упорядоченные подмножества (цепочки) элементов множества S. Выражение (1.1) будем называть описанием QS si, а само обозначение si именем QS . Множество Ii будем называть множеством входов QS , а множество Oi — множеством выходов QS . Элементы sj О Ii будем называть родителями или предками si , а sj О Oi – потомками. Связи, определяемые Ii и Oi, будем называть квантово-структурными связями (QS-связи) соответственно входными и выходными. Все множество множеств Ii и Oi будем обозначать как I(S) и O(S) соответственно. 1.2. Типы квантов структуры. Из рис.1 видно, что в S можно выделить четыре типа QS характеризующихся наличием или отсутствием входных и выходных связей. Первый тип. QS, не имеющие ни входов, ни выходов, будем называть пустыми или нуль-квантами. Подмножество нуль-квантов в S будем обозначать как N(S). Второй тип. QS, имеющие только выходы, образуют в S подмножество B. Элементы B будем называть базовыми QS, а само подмножество B базой QSS и обозначать как B(S). Будем говорить, что S построено над B или порождено B. Третий тип. QS, имеющие как входы, так и выходы, будем называть внутренними или полными QS, а их подмножество обозначать как D(S). Четвертый тип. QS, имеющие только входы, будем называть вершинами QSS, а их подмножество обозначать как W(S). 1.3. Функции и операции над QSS . Каждый QS характеризуется количеством входных и выходных связей. Количество входов или выходов QS si , как принято в теории множеств, будем обозначать card Ii и card Oi соответственно [1]. Модифицированные в процессе вычислений значения будем обозначать знаком "~" в качестве верхнего индекса соответствующей переменной. QSS S будем называть полным, если выполняется следующее условие: card W(S) = 1. (1.2) В полном QSS существует одна и только одна вершина. Расширим понятие базы. В отличие от базы QSS B(S) относительной базой B будем называть любое заданное подмножество:
1.3.1. Функции конвергенции и дивергенции. Пусть дано QSS S элементов (si / Ii / Oi). Определим на S функцию конвергенции QS si как: con(si) = card Ii . Аналогично определим функцию дивергенции QS si как: div(si) = card Oi . 1.3.2. Функция обратной дивергенции (QS-вероятность). Определим функцию обратной дивергенции qsp(si) (функция QS-вероятности) как функцию обратную к div(si):
Можно утверждать, что функция (1.3) численно выражает меру неопределенности (QS-вероятности) при выборе пути на графе QSS из вершины si; или характеризует степень принадлежности данного кванта структуры к каждому из порожденных им QS потомков; или характеризует силу (потенциал) связи между элементами QSS родителями и потомками. 1.3.3. Функция текущего состояния. Введем в рассмотрение также некоторую функцию act(si) , которую определим следующим образом:
Значение функции act(si) будем называть текущим состоянием QS si, а множество состояний всех QS текущим состоянием QSS и обозначать как act(S). 1.4. Прямое QS-преобразование (QS-свертка). Пусть задано QSS S и его линейно-упорядоченное подмножество:
Определим QS-свертку следующим образом:
При n = 2 будем говорить о бинарной QS-свертке и записывать как si Е sj . При n = m будем говорить об m-арной QS-свертке. Результатом QS-свертки является QS с описанием, соответствующим (1.4). 1.5. Обратное QS-преобразование (обратная L-проекция). Пусть задано QSS S и его линейно-упорядоченное подмножество:
Тогда обратную L-проекцию L(P) определим как:
Результатом обратной L-проекции является упорядоченное множество (цепь) родителей P. Если цепочка P состоит из одного si , то L(si) есть обратная L-проекция si. Соответственно n-ую обратную L-проекцию определим как:
Относительной обратной L-проекцией si относительно заданной базы B будем называть минимальную n-ю обратную L-проекцию, удовлетворяющую условию:
Полной обратной L-проекцией si будем называть минимальную n-ю обратную L-проекцию, удовлетворяющую условию:
Результатом полной обратной L-проекции является упорядоченная цепочка базовых прародителей данного QS. В силу определения (1.5) для любого si О S существует одно и только одно значение LS(si). 1.6. Понятие уровня в QSS. Относительным уровнем UB(si) QS si в QSS S будем называть такое min число n, при котором " sj О Ln(si) О B . QS sj О B будем называть QS нулевого уровня относительно базы B. Абсолютным уровнем QS si будем называть такое min чило n, при котором " sj О Ln(si) О B(S). QS sj О B(S) будем называть QS нулевого уровня QSS S. Уровнем QSS U(S) будем называть max из абсолютных уровней QS si О S. 1.7. Линейное равенство и эквивалентность в QSS. Введем понятие линейного равенства (L-равенство) и линейной эквивалентности (L-эквивалентность) QS. Пусть заданы S1 и S2 над базой B , а также si О S1 и sj О S2 . Два QS L-равны относительно B тогда и только тогда, когда они имеет равные обратные QS-преобразования относительно B, т.е. si =B sj , если LB(si) = LB(sj). Будем говорить, что S1 L-эквивалентно S2 относительно базы B, если для любого si О S1 в S2 существует такой sj О S2 , что si =B sj и будем записывать это как: S1 МB S2 . Два QSS S1 и S2 L-равны относительно базы B тогда и только тогда, когда все QS из S1 или S2 имеют взаимно равные полные обратные QS-преобразования в другом QSS относительно заданной базы, т.е. S1 =B S2 , если S1 МB S2 и S2 МB S1 .
Из рис.2 видно, что все три изображения QSS имеет разную внутреннюю топологию, однако можно утверждать, что S1 М B S2 и S1 М B S3 т.к. все QS S1 имеют в S2 и S3 тождественные обратные QS-преобразования относительно базы B = {s1 , s2 , s3 , s4} . Очевидно, для любого QSS S1 такого, что $ si О S1 имеют con(si) > 2 существует L-эквивалентное QSS S2 такое, что " si О S2 имеют con(si) Ј 2. Такое QSS будем называть бинарным.
|
|
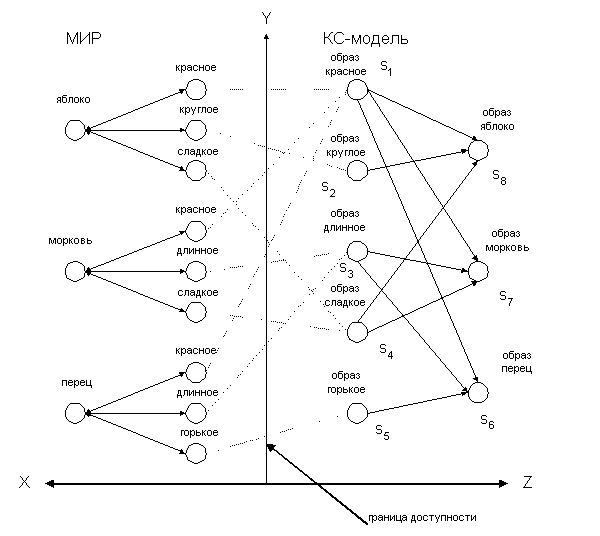
2. Квантово-структурная и линейная информационные модели физического мира. 2.1. Определение QS-модели и основные гипотезы КСТ. На рис.3. изображен ограниченный физический Мир и его QS-модель. Точнее будет сказать, что Мир изображен в виде модели (назовем ее линейной или L-моделью), которая соответствует общепринятой логике или здравому смыслу.
Когда вы видите перед собой красное и круглое яблоко, интуитивно вы чувствуете, что это красное принадлежит именно этому конкретному яблоку. Когда перед вами на столе лежат десять красных яблок, это осознается в виде красочной фотографии, где каждое яблоко со своим красным занимает вполне определенное место. Вы видите десять "красное" и каждое на своем месте. Таким видит физический мир наше сознание. Рассмотрим, насколько это соответствует действительности. Если представить множество "датчиков" способных на физическом уровне воспринимать События внешнего мира в виде линии, то это и будет та граница доступности, посредством которой физический мир существующий вне нас доступен нам объективно. Действительно, объективно (на физическом уровне) мы можем "видеть", условно говоря, только <красное>, <круглое>, <сладкое>. Само <яблоко> – как физический объект, мы "видеть" в принципе не можем. Понятие объективно следует взять в кавычки потому, что абсолютно объективно мы не можем "видеть" ни <красное>, ни <круглое>, ни <сладкое>, ни что-либо другое. Это тоже образы, объективность которых определяется достоверностью (качеством) работы наших органов чувств. Мир, который мы осознаем, как некую объективность, принципиально для нас может быть только субъективным, так как граница объективности проходит где-то левее границы доступности. Следовательно, рассматривая "качество" Модели, говорить следует об ее адекватности в том смысле, что Модель по своему объему (Y, Z) достаточна для достижения поставленной цели в данном конкретном Мире. Какие бы сложные События не происходили во внешнем мире, на физическом уровне доступны они нам будут лишь как некоторое множество элементарных (базовых) Событий, их комбинаций и (или) последовательностей. Отношения между физическими Событиями доступны также только через линию доступности, т.е. в виде отношений тех же базовых Событий, их комбинаций или последовательностей. Эти рассуждения и положены в основу QS-модели. Считаем, что физический Мир в силу своих законов порождает только ему присущее QSS. Обозначим это QSS как M. Тогда под QS-моделью в общем случае будем называть QSS M, отображающее в своих QS-связях закономерности физического мира, а QS-моделью в узком смысле некоторое его подмножество S построенное относительно заданной базы B такое, что S М B M или S =B M. Как известно, "всякая модель тогда чего-нибудь стоит …". Поэтому в качестве рабочих мы определим две гипотезы и попробуем убедить в их правильности. Гипотеза 1. QS–модель позволяет адекватно отображать все закономерности физического мира. Гипотеза 2. QS–модель реализована природой в виде биологических нейронных структур (сетей). 2.2. Понятие информации с позиций КСТ. Под количеством информации понимается мера снятия неопределенности в процессе получения сообщения (События) наблюдателем. Последовательность рассуждений при этом следующая: есть наблюдатель, есть неопределенность исхода, в результате опыта неопределенность изменилась, следовательно, наблюдатель получил какое-то количество информации. Представим себе наблюдателя, которому априорно известна QS-модель изображенная на рис. 3. Его задача идентифицировать События внешнего мира исключительно на основе QS-модели и получаемой информации. Предположим, что наблюдатель видит <красное>. Образ s1 связан в модели со всеми тремя образами физических объектов s6 … s8. Все три объекта имеют равные права быть выбранными. Неопределенность ситуации не изменилась. До опыта равновероятны были все три объекта и после опыта мы не можем утверждать что-либо другое. Следовательно, признак <красное> в данном Мире для наблюдателя не несет никакой информации (Мир, который мы определили как цветной, фактически оказался для наблюдателя черно-белым). Напротив, признак s2 связан лишь с одним из всех возможных объектов. Следовательно, наблюдая <круглое> наблюдатель снимает неопределенность ситуации полностью. Можно утверждать, что в данном случае QS s2 имеет максимально возможную информативность для наблюдателя или несет максимально возможное количество информации, которое может переносить один QS — одну единицу или один квант информации. Образ или признак s3 связан в модели с двумя образами объектов. Следовательно, после наблюдения s3 неопределенность ситуации уменьшается. Остается неопределенность выбора двух объектов из трех возможных. В этом случае информативность QS s3 меньше, чем s2. Можно сделать вывод, что, информативность или количество информации, получаемое наблюдателем, обратно пропорционально функции дивергенции QS. А это, по нашему определению, есть функция QS-вероятности qsp(si). Таким образом, количество информации, получаемое наблюдателем в процессе взаимодействия с внешним Миром, есть величина субъективная (относительная), так как зависит от его априорных знаний об этом мире — знаний QSS. С другой стороны, можно утверждать, что независимо от того есть наблюдатель или его нет, информация в Мире, равно как и в его QS-модели, существует объективно и заключена она в самой структуре Мира. 2.3. Линейная информационная модель. Известно что, как разговорный, так и письменный язык являются носителями наших знаний, т.е. способом отображения, хранения и передачи информации обо всех известных нам закономерностях физического мира. Представьте себе, что мы взяли все, что когда-либо было написано и напечатано, т.е. отображено с помощью письменного языка и выстроили бы в одну линию P. Такая конструкция представляла бы из себя очень длинную, но все же конечную упорядоченную цепочку символов алфавита языка, включая и его разделительные знаки. Фактически письменный язык можно определить как линейную информационную модель (L-модель) физического мира, где каждому Событию соответствует слово или последовательность слов языка, составленных из знаков алфавита данного языка и разделенных специальными знаками алфавита — разделителями. К недостаткам L-модели можно отнести повторяемость элементов, последовательный доступ и полное отсутствие того, что мы называем ассоциативностью. 2.4. Квантово-структурная информационная модель. Рассмотрим возможности QS-модели как модели отображения информации. Для любого полного QSS (1.2) существует единственная полная обратная L-проекция его вершины. Следовательно, можно утверждать, что и для нашей цепочки P существует ее QS-эквивалент, точнее целый класс L-эквивалентных P QSS. Таким образом, все наши знания (все, что нам известно о закономерностях физического мира), заключенные в L-модели P, могут быть сохранены в QS-модели, а полная обратная L-проекция ее вершины гарантирует нам их последующее воспроизведение в первоначальном виде без каких-либо потерь. Отметим особенности такого способа отображения информации. Можно показать, что среди множества L-эквивалентных QSS существует такое отображение, где каждое информационное Событие будет представлено в QS-модели в виде отдельного и при этом единственного QS. Другой особенностью является независимость сложности QS (количество входов и выходов) как носителя информации от его линейного эквивалента и сложности отображаемого им События. В QS-модели информационные События связаны между собой, что делает возможным осуществление не только операций запоминания и воспроизведения информации, но и ассоциативных операций типа распознавания и др. |
|
3. Квантово-структурные машины. Продолжим наш опыт с наблюдателем. Допустим, что наблюдатель умеет запоминать и накапливать полученную информацию в ходе эксперимента. Тогда, увидев <длинное>, наблюдатель рассчитает QS-вероятность выбора: <яблоко> — 0; <морковь> — 0,5; <перец> — 0,5 . Продолжив исследование физического мира, наблюдатель в какой-то момент "увидит" <сладкое> и после несложного расчета будет иметь следующую информацию для принятия решения: <яблоко> — 0,5; <морковь> — 1,0; <перец> — 0,5. Выбрав объект, для которого сумма QS-вероятностей максимальна, наблюдатель поступит абсолютно разумно. Нетрудно заметить, что выше сказанное описывает процесс принятия решения на основе текущего состояния QS-модели act(S). При этом наблюдатель воспользовался принципом максимума QS-вероятности. Отметим, что в качестве меры QS-вероятности может использоваться любая монотонно-убывающая функция от дивергенции. Снабдим нашего наблюдателя простой программой действия: <яблоко> — <съесть>; Тогда, следуя этим формальным правилам, он сможет не только безошибочно распознавать объекты, но и разумно действовать, что позволит ему, например, выжить в данном Мире. Заметим, что во всех случаях наш наблюдатель в интеллектуальном плане действовал абсолютно формально в соответствии с QS-моделью. Если в нашем распоряжении есть входное устройство, способное распознавать базовые События (<красное> и т.д.), и выходное устройство, способное реализовывать принцип MAX и программу (3.1), то мы вполне можем заменить наблюдателя машиной, изображенной на рис.4.
В данном устройстве автомат описывается единственной функцией act(S). Можно показать, что поведение машины ничем не будет отличаться от поведения нашего наблюдателя в данном описанном нами Мире. Такие машины мы будем называть QS-машинами первого типа или неадаптивными QS-машинами. В отличие от первых, машинами второго типа – адаптивными или самообучающимися будем называть QS-машины, дополнительно имеющие возможность реализации алгоритма, позволяющего на основе регистрации базовых Событий формировать внутри себя QS-модель адекватную QSS физического Мира. |
|
4. Квантово-структурная модель биологических нейронных систем. Можно считать, что механизмы функционирования биологических нейронных сетей в физиологическом аспекте исследованы достаточно хорошо. Однако убедительного ответа на вопрос: "Какие информационные принципы лежат в основе работы БНС?" — до настоящего времени нет. В качестве альтернативы предлагается следующая информационная модель функционирования БНС: 1) БНС является биологической реализацией QS-модели отображения внешней по отношению к ней среды по принципу "один в один": один нейрон — один квант структуры — одно Событие. 2) Связи между нейронами морфологически соответствуют QS-связям модели и выполняют функцию долговременной памяти. 3) Состояние активности отдельного нейрона описывается функцией состояния QS act(si). 4) Состояние активности всей НС соответствует состоянию QSS act(S) и выполняет функцию кратковременной памяти. 5) Множество нейронов сенсорной группы образуют базу QSS B(S). 6) Формирование QS-связей между нейронами (замыкание связей) осуществляется по принципу QS-свертки. 7) Реализация принципа максимума QS-вероятности qsp(si) осуществляется с помощью тормозных процессов НС. Предполагается, что существует адекватное внешней среде количество нейронов и потенциально-возможных связей между ними, которые и реализуются в процессе функционирования БНС. 5. Заключение. Способность отображать События физического мира и их взаимосвязи в виде QSS наряду со способностью на основании текущего состояния act(S) действовать в соответствие с принципом MAX QS-вероятности, по мнению автора, и являются той самой информационной первоосновой явления называемого интеллектом. Список литературы 1. Г. Корн и Т. Корн. Справочник по математике для научных работников и инженеров, М., Наука, 1973г. © В.Н. Свиридов 2000. |
|
|
|
© 2000 Design by Asart. |

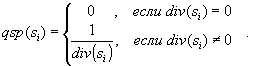 (1.3)
(1.3)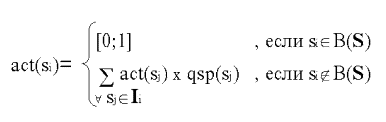
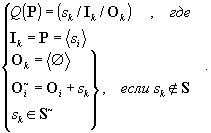 (1.4)
(1.4)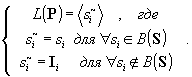 (1.5)
(1.5)